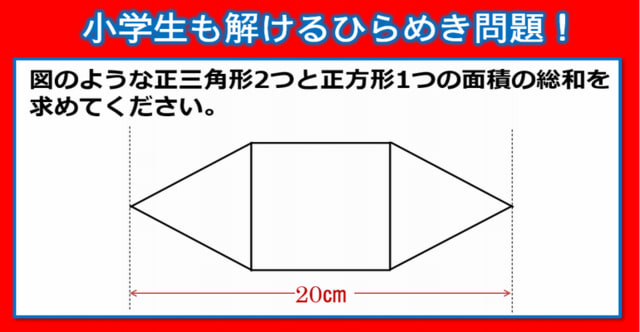
三 平方 の 定理 小学生 279675
図形 角度 面積問題 三平方の定理 中学生 練習問題45 60 75 3 4 5 の三角形 みんなの算数クラブ
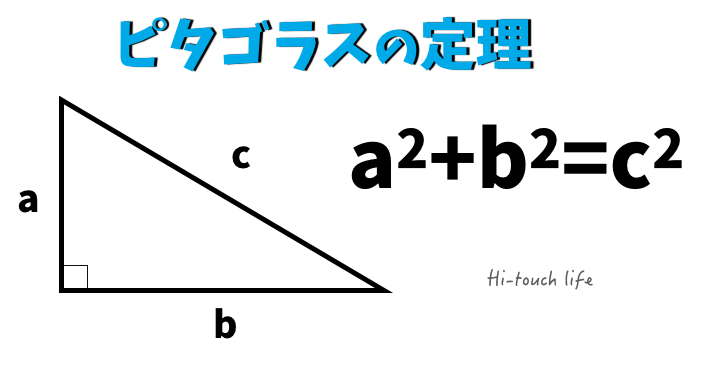
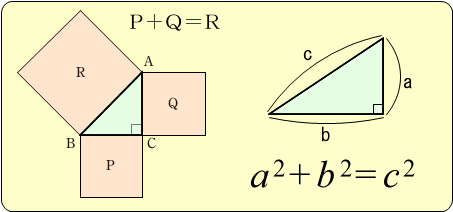
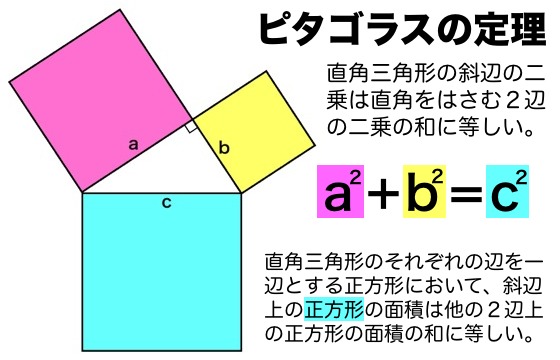
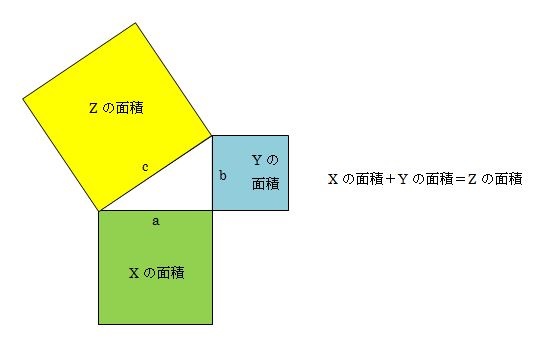
三平方の定理の解説 直角三角形における3辺の長さによる定理を 三平方の定理 (さんへいほうのていり)と言います。 ピタゴラスの定理とも言われます。 三平方の定理では、直角三角形の斜辺をc、その他の辺をそれぞれa、bとした場合に、 a 2 b 2 = c 2 が成り立ちます。 2110 1 三 平方 の 定理 小学生 コメントを投稿 続きを読む 50 可愛い トート バッグ 作り方 リンクを取得
三 平方 の 定理 小学生
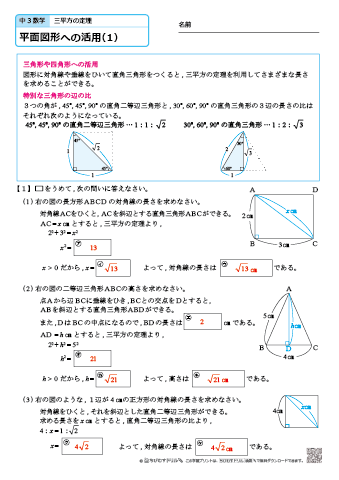
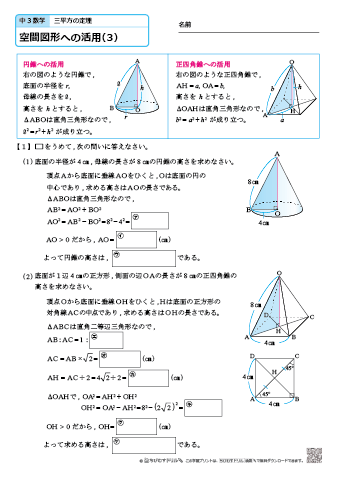
三 平方 の 定理 小学生-動画一覧や問題のプリントアウトはこちらをご利用ください。 数学中361 三平方の定理①(基本編) Watch later Share Copy link Info Shopping4 三平方の定理の応用問題 5 底面の半径が 2 cm,母線の長さが 8 cm の円錐について,次の問いに 答えよ。 ⑴ 側面の展開図のおうぎ形の中心角を求めよ。 ⑵ 右の図のように,円錐の側面上をまわるように,点 A から点 A ま でひもをかける。

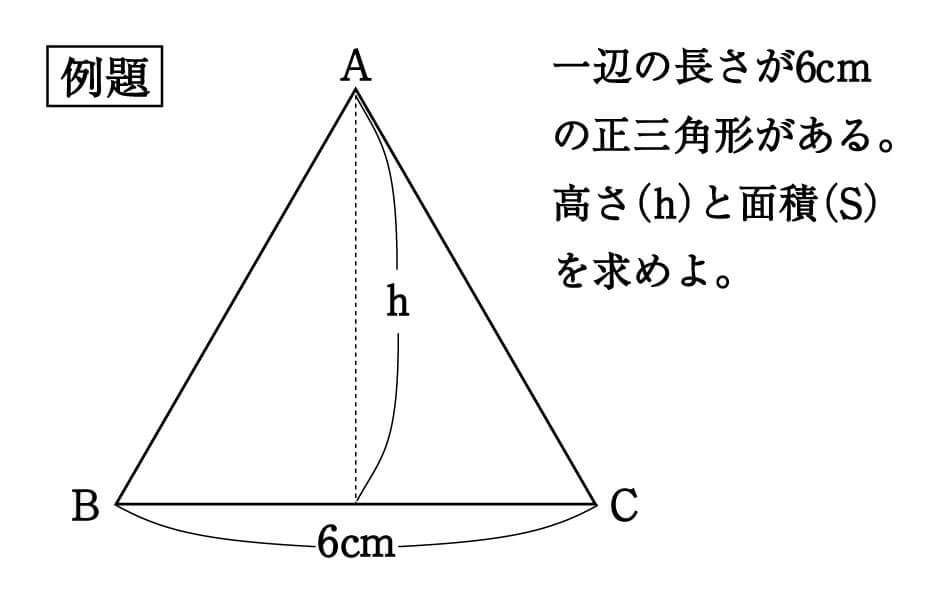
簡単計算 二等辺三角形の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
つまり、下図のようになるよ! ということは、各頂点から点Pまでの長さが 6 6 だから、三平方の定理を用いると、 x2 = 62 –22 x 2 = 6 2 – 2 2 ∴ x2 = 36− 4 = 32 x 2 = 36 − 4 = 32 ∴ x = 4√2 x = 4 2 (x>0より) これを図にするとこう! 終わり! はかせちゃん お疲れ 三平方の定理の証明は、紀元前からあらゆる人があらゆる方法で考え出してきました。 この記事では、「モナ・リザ」や「最後の晩餐」で有名な 芸術家レオナルド・ダ・ヴィンチが考案した証明方法 を、 現役数学教員がわかりやすく解説 します。 ユークリッドと同様の図に補助線を加え三平方の定理(ピタゴラスの定理)と公式の証明忍者が用いた三角の知恵 が成り立つことを、 三平方の定理 と言います。 三平方の定理は、別名「ピタゴラスの定理」とも言います。 例えば、直角をはさむ2つの辺の長さが 3 c m と 4 c m の直角三角形
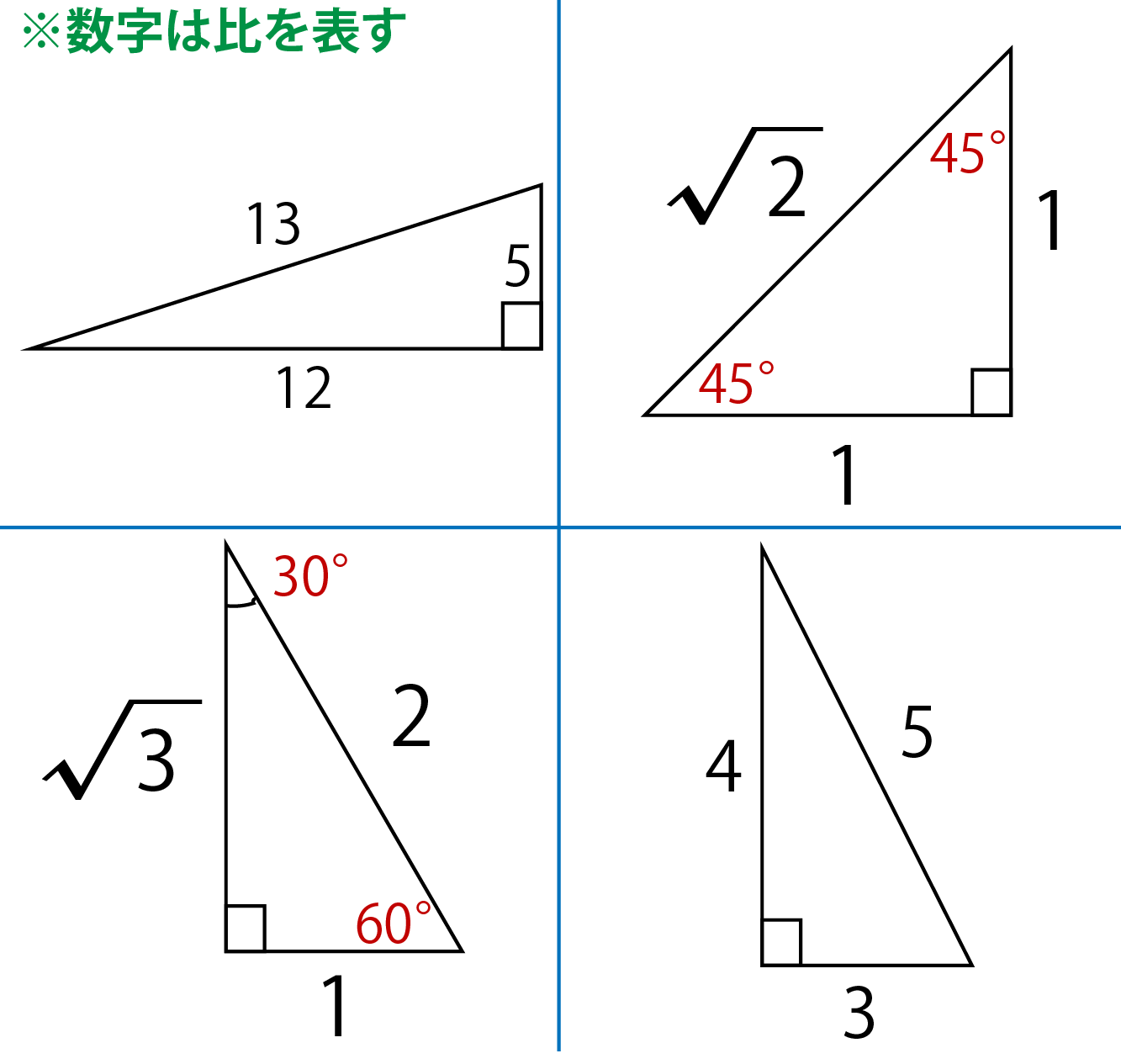
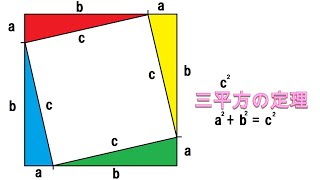
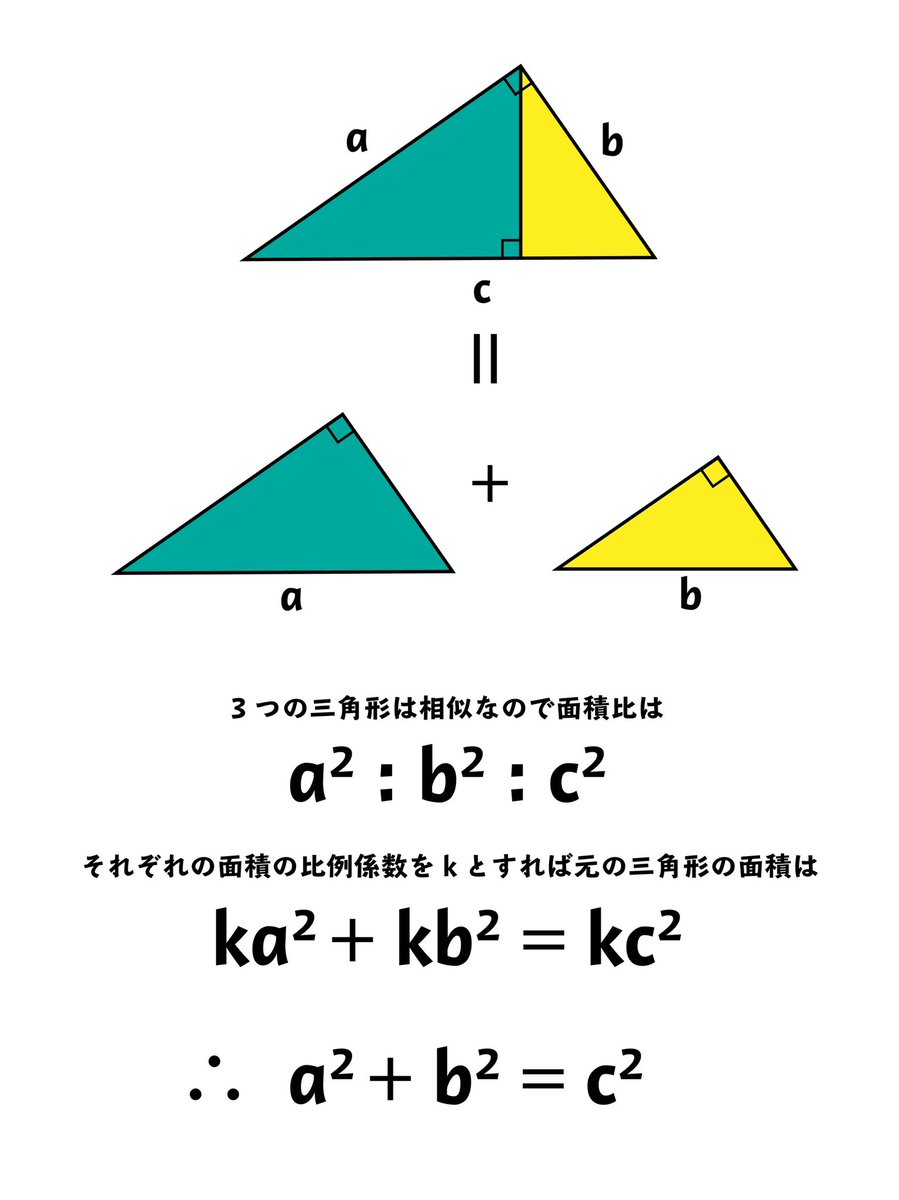
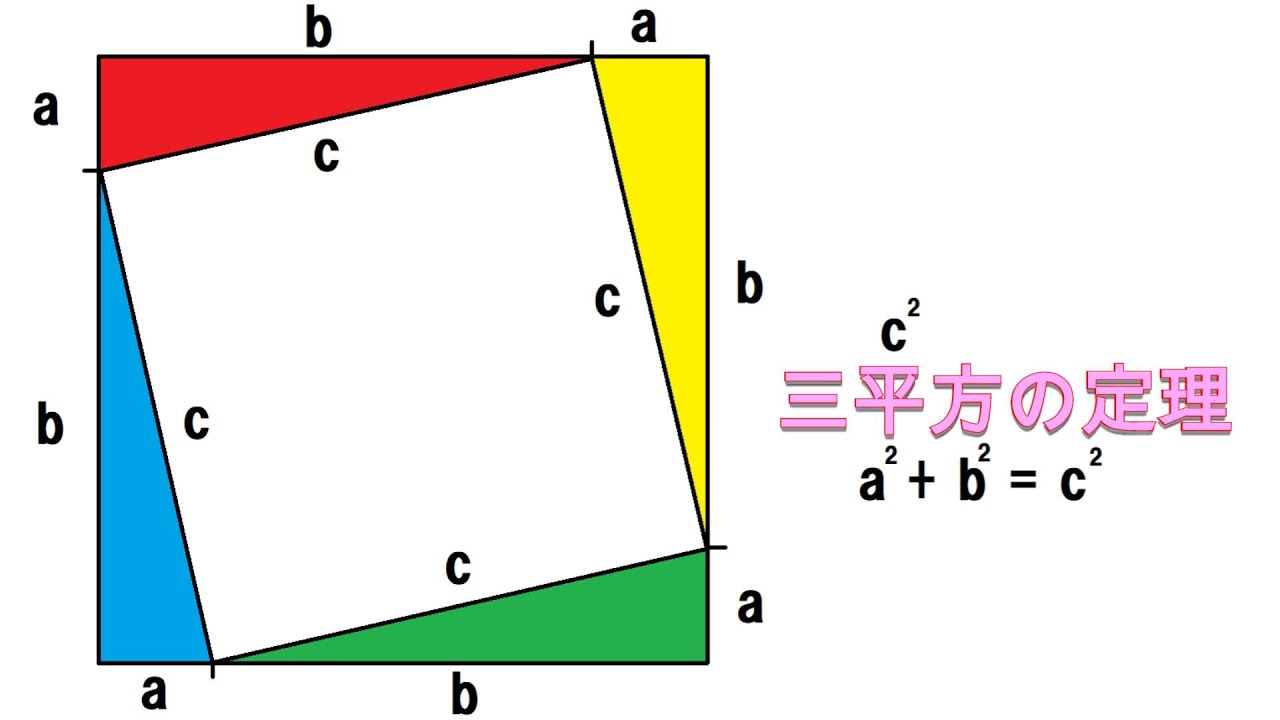
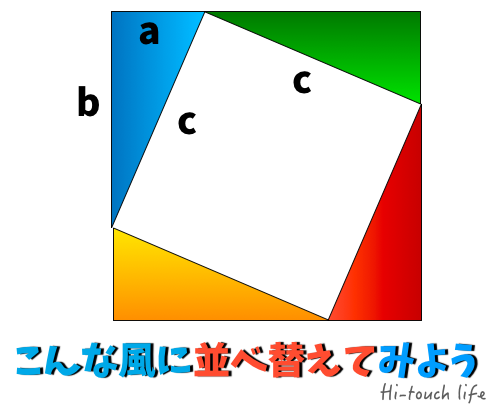
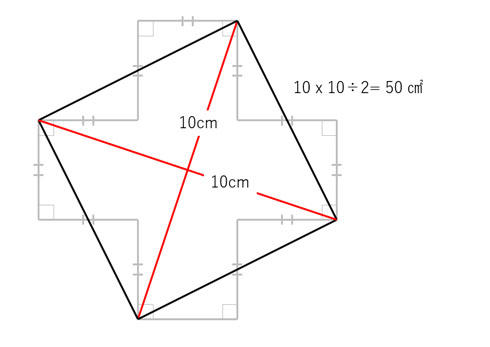
三平方の定理とは 三平方の定理(基本問題1) 例題と練習 三平方の定理(基本問題2) 例題と練習 三平方の定理(四角形の対角線) 例題と練習 特別な三角形 例題と練習 特別な三角形2 例題と練習 二等辺三角形の面積 例題と練習 三辺から三角形の面積を求める 例題と練習 座標上の2点間の距離 例題と 三つの平方数の和 三角数定理の証明に用いる定理を紹介します。 8 8 8 で割って 3 3 3 余る正の整数は三つ以下の平方数の和で表せる (ルジャンドルの結果の特殊な場合)三平方の定理 直角三角形の三辺の長さを a、b、c とすると、 正方形P の 面積 c 2 は a+b を 1辺 とする正方形の面積から 4 つの合 同な直角三角形の面積を引いたものと等しいよね。 だから、 正方形P の面積は次のよう
三 平方 の 定理 小学生のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  | |
「三 平方 の 定理 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「三 平方 の 定理 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
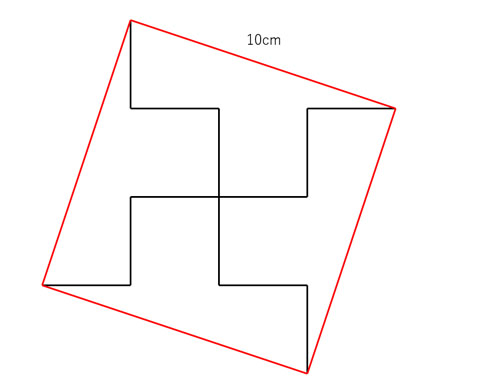 |  | |
「三 平方 の 定理 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
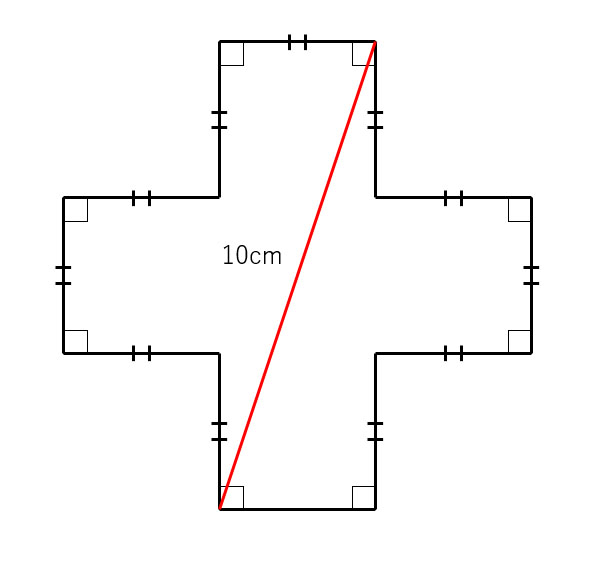
 |  | |
 |  | 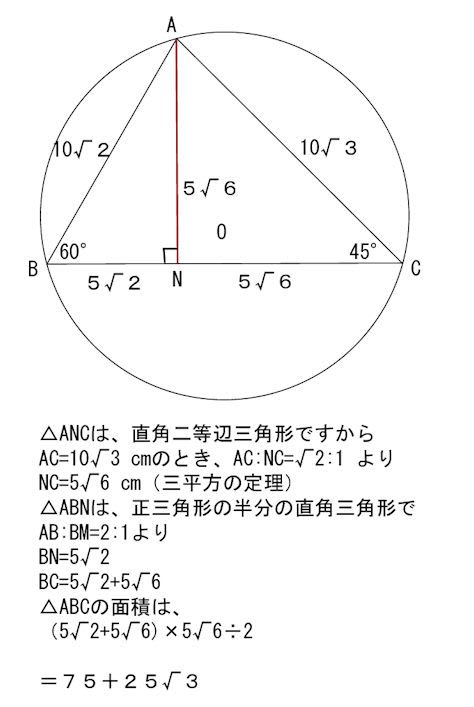 |
 |  | |
「三 平方 の 定理 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「三 平方 の 定理 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 | ||
「三 平方 の 定理 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「三 平方 の 定理 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三 平方 の 定理 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
「三 平方 の 定理 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三 平方 の 定理 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | ||
「三 平方 の 定理 小学生」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |
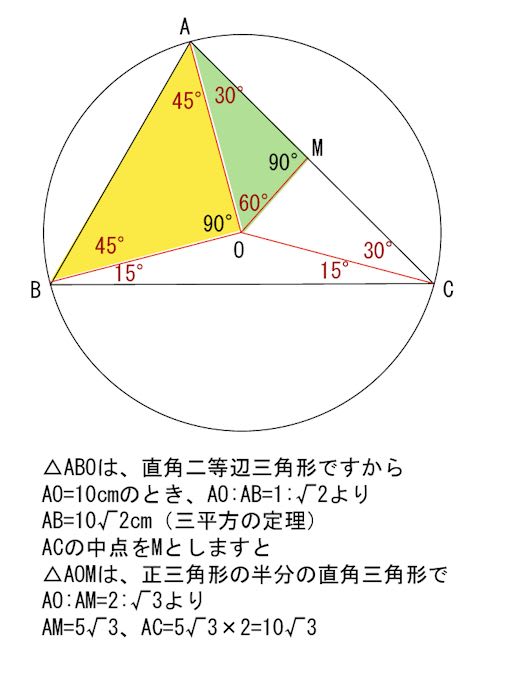
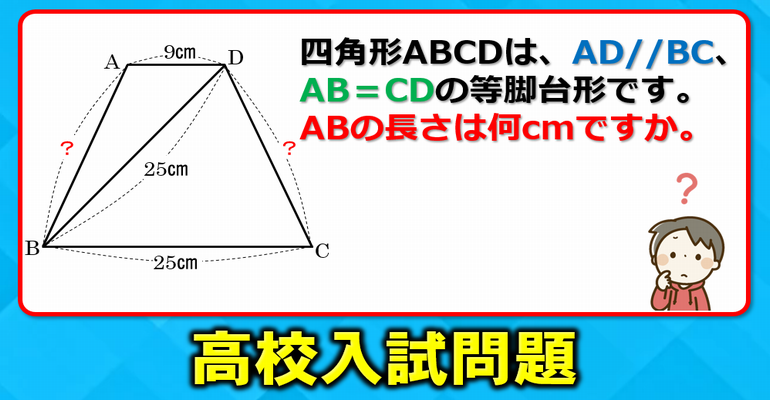
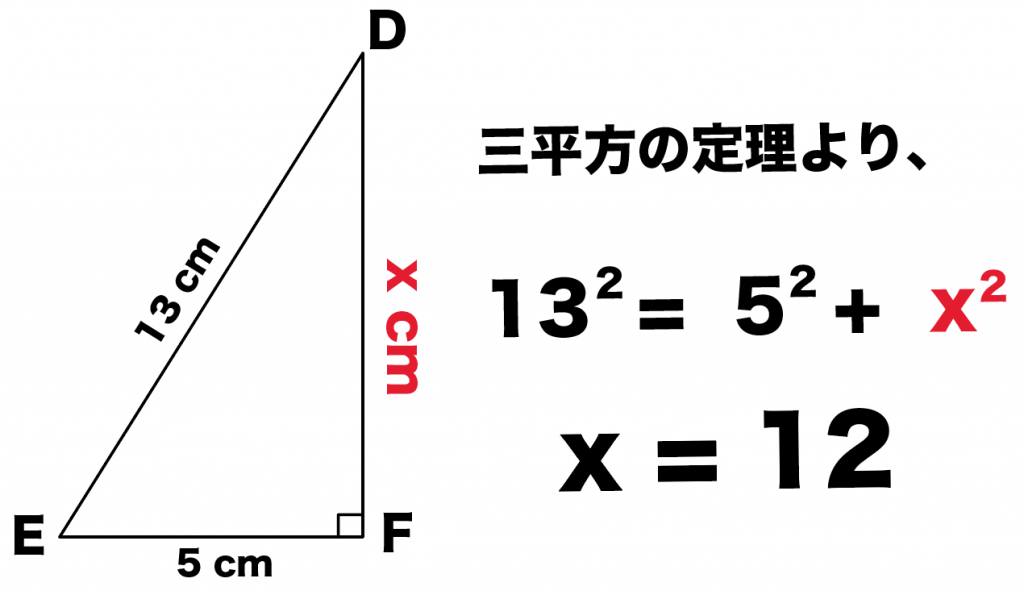
三平方の定理より、これらを足し合わせたもの、 つまり=4225が xの2乗に等しくなります。 さて、4225の平方根って何だろう?って話ですが、 地道に探すのはあまり賢くなさそうです。 ここで注目するのが4225という数字。 以下の図のようになるのでしょうか。 先に結論を紹介すると「 なります 」。 なぜなら三平方の定理から次のことが成立するからです。 ( 2 倍× 2 ) 2 =( 2 倍×√3) 2 +( 2 倍× 1 ) 2 これを展開すると、このようになります。 16 = 12 + 4 では 2 倍
コメント
コメントを投稿